TEXTO VIII: Exercícios Iniciais de Lógica Simbólica

Rodrigo Rodrigues Alvim

Antes da leitura deste texto, aconselha-se a leitura do Texto XVIII (Elementos de Lógica Simbólica), dentro da categoria Lógica.

Construam as tabelas de verdade dos seguintes enunciados:

p . ~ p

~ (p . ~ p)

Percebam que o resultado alcançado para (p . ~ p), em todas as possibilidades, foi sempre “falso” (F) e para [~ (p . ~ p)], em todas as possibilidades, foi sempre “verdadeiro” (V). Sempre quando um enunciado composto obtiver esse primeiro resultado em todas as suas possibilidades, tratar-se-á de uma contradição; sempre quando um enunciado composto obtiver esse segundo resultado em todas as suas possibilidades, tratar-se-á de uma tautologia. Caso tivermos ambos os resultados, tratar-se-á de uma contingência.

Observem que o segundo enunciado é a fórmula do princípio de contradição (também chamado de princípio de não-contradição), princípio lógico que corresponderia ao princípio ontológico, segundo o qual não pode “algo” ser e não ser ao mesmo tempo e sob a mesma relação: se “algo” designa um objeto, a definição se dá no campo ontológico; se “algo” se refere a uma proposição, a definição se dá no campo lógico (“não , ao mesmo tempo, p e não p”).

Construam agora as tabelas de verdade dos próximos enunciados:

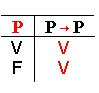
p → p

p ↔ p

Como a tautologia definidora do princípio de não-contradição, estas tautologias imediatamente acima definem o princípio de identidade.

Construam igualmente a tabela de verdade do enunciado abaixo:

p v ~ p

Trata-se também de uma tautologia? Pois bem, este enunciado é a fórmula do princípio do terceiro excluído.

Como próxima tarefa, construam as tabelas de verdade dos três enunciados subseqüentes:

(p . q) → p

~ [p → (p v q)]

~ (p . q)

Pelos resultados obtidos, respondam se cada um dos enunciados acima é “tautológico”, “contraditório” ou “contingente”.

Construam também as tabelas de verdade dos dois novos enunciados:

[(p → q) . p] → q

[(p → q) . ~ q] → ~p

Estas fórmulas supracitadas (ambas tautológicas, como se vê) são chamadas, respectivamente, de “modus ponens” e de “modus tollens”. Comumente, são também apresentadas das seguintes maneiras:

p → q
p
--------
q


p → q
~ q
---------
~ p

Construam a tabela de verdade de (p → q) e marquem, para cada um dos argumentos acima, a única linha onde seria possível observar e demonstrar a necessidade de cada conclusão.

Elaborem as fórmulas (enunciados compostos) dos seguintes argumentos:

p → q
q
--------
p

p → q
~ p
---------
~ q

Construam as tabelas de verdade das fórmulas (enunciados compostos) então elaboradas.

Pelos resultados obtidos, respondam se cada uma das fórmulas (enunciados compostos) acima é “tautológico”, “contraditório” ou “contingente”.

Construam a tabela de verdade de (p → q) e marquem, para cada um desses dois últimos argumentos, as duas linhas pelas quais seria possível observar e demonstrar a contingência de cada conclusão.

Espero que estes exercícios lhes tenham sido mais que uma oportunidade de auto-avaliação. Noutros termos, espero que estes exercícios lhes tenham sido também uma oportunidade de novas aprendizagens.